The Matérn Kernel: Part I

A kernel implementation for rough stochastic processes.

In this post I will be talking about kernels, and particularly the Matérn kernel which can be used to model stochastic time series with rough fractal-like characteristics and long-range dependencies.

Kernels in Machine Learning

Kernels are essentially functions over the input in non-linear, high-dimensional space. They are a non-parametric approach that can scale up parameters as the data grows in complexity. They are used in a wide range of applications such as image processing and generation, natural language processing, and they also play a role in the attention mechanism: part of the architecture of transformers used in new foundation models (LLMs) such as ChatGPT. These models rely on attention mechanisms to weigh the importance of different parts of the input sequence with respect to the learning objective.

When you carry a conversation with ChatGPT that refers back to the same concept, or some contextual content, it uses the dependence between the latent states of the input to relate the context of those prompts. In transformers this is achieved in part with a kernel (see the references listed at the end of the post for details).

Why Attention Matters

In their paper Attention Is All You Need, the authors introduce self-attention mechanisms, which allow a model to weigh the importance of different components of the input space when making inferences. This attention mechanism releases a model from limitation by a fixed window size or sequential, strictly Markov processing.

The attention mechanism is fundamentally non-Markovian which means that in order to know the next state of the system you need to know it’s entire history. When you prompt ChatGPT during a long conversation, referring back many times to previous concepts or points of discussion, ChatGPT must pick out these conversational components correctly in their context. It needs to know the entire history of the discussion around that concept up until that point.

This matters in the context of the problem of sequence transduction generally meaning any task where input sequences are transformed into output sequences. In the case of generating a synthetic approximation of a real time series, if the original contains an auto-correlation structure then the copy needs to contain a similar structure to be realistic.

Auto-Covariance and LRD

Rough stochastic processes are often characterized by the presence of auto-correlation or long-range dependence which can be analyzed as an auto-covariance matrix.

\(\mathbf{\Sigma} = \begin{bmatrix} \gamma(0) & \gamma(1) & \gamma(2) \\ \gamma(1) & \gamma(0) & \gamma(1) \\ \gamma(2) & \gamma(1) & \gamma(0) \end{bmatrix} \)

The auto-covariance function is a measure of the covariance of data points at increasing lags. Where the H parameter below is the Hurst exponent, one way we will be able to measure auto-correlation and LRD in synthetic data.

\(\large cov(x_1,x_t) = \frac{1}{2} \left( x_t^{2H} + x_1^{2H} - |x_t-x_1|^{2H} \right)\)

By intentionally introducing auto-correlation the result is a slow decay (LRD) that is related to a latent effect and the goal is to see if we can detect this effect using a latent state model. Markov-switching data generating processes, such as the Dirichlet process mixture model, may assume independence between the latent states, which breaks the auto-correlation between the samples and leads to an inaccurate synthetic dataset with respect to the auto-correlation structure or LRD structure.

Sine Waves

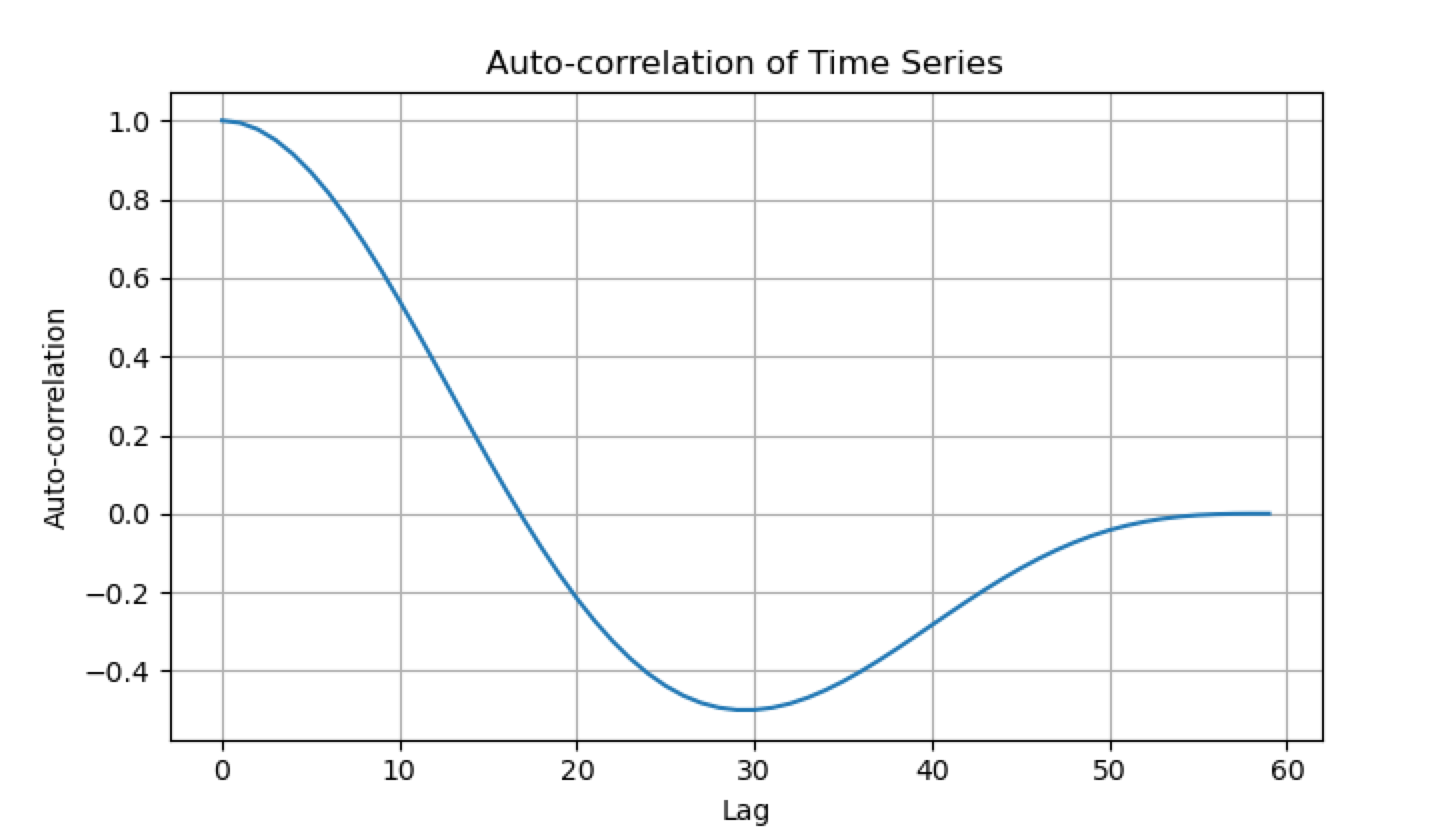
Sine waves serve as an intriguing example of auto-correlation within time series data in an obvious and trivial way. When examining sine waves, we can observe a distinct form of auto-correlation that gradually decays towards zero.

auto-correlation decay of a sine wave

Sine waves are characterized by their periodic nature with an amplitude and frequency of the wave cycle. In the case of sine waves, this persistence is evident as the wave oscillates through multiple cycles.

The sine wave is also a continuous and smooth infinitely differentiable function. Kernels can also be used to model more discrete time series with rough characteristics and sudden jumps. This is achieved via the lengthscale argument and the smoothness argument of the Matérn kernel.

The former controls how far into the future the decay process of the auto-correlation lasts, and the latter controls the differentiability of the data.

Matérn Kernel for Rough Processes

\(k(x_i, x_j) = \frac{1}{\Gamma(\nu) 2^{\nu - 1}} \left( \frac{\sqrt{2 \nu}}{l} d(x_i, x_j) \right)^{\nu} K_{\nu} \left( \frac{\sqrt{2 \nu}}{l} d(x_i, x_j) \right)\)

where,

• d(xi, xj)) is the Euclidean distance between points xi and xj,

• Kν(⋅) is the modified Bessel function of the second kind,

• Γ(ν) is the Gamma function,

• l is the lengthscale parameter,

• ν controls the smoothness of the function (smaller ν gives less smooth functions).

The Matérn kernel can model a range of rough stochastic processes, particularly when the smoothness parameter is small.

Types of Stochastic Processes

• Ornstein-Uhlenbeck Process (ν = 1/2): When the Matérn kernel is set with ν = 1/2, it becomes the exponential kernel, which models extremely rough (nowhere differentiable) sample paths. This is often called the Ornstein-Uhlenbeck process in continuous time, and in many cases, sample paths from this process are highly jagged and lack any smoothness.

• Processes with ν < 1: As the Matérn ν parameter approaches zero, the modeled processes become even rougher; sample paths display random, non-smooth structure at every scale, exhibiting properties similar to fractal curves or fractional Brownian motion with high-frequency roughness.

• General non-differentiable processes: For any ν ≤ 1/2, Matérn kernels generate Gaussian processes whose realizations are not even once mean-square differentiable—useful for modeling geostatistical or environmental signals, turbulent flows, and noisy sensor data where observations change abruptly over short distances or timescales.

Auto-Covariance Matrix

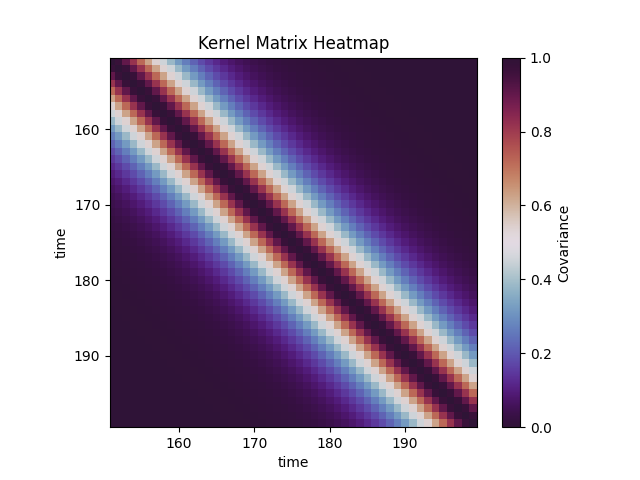
I will be using the Matérn kernel to capture the auto-covariance structure of some one dimensional time series data by starting with a self-similarity matrix: similarities between each data point and all available pairwise relationships in sequential time. A lagged cross-correlation matrix of the 1D series with itself for all possible starting points and lags.

Zooming in reveals how the covariance, in this case auto-covariance, decays away slowly from any origin point as time passes.

kernel matrix (zoomed in)

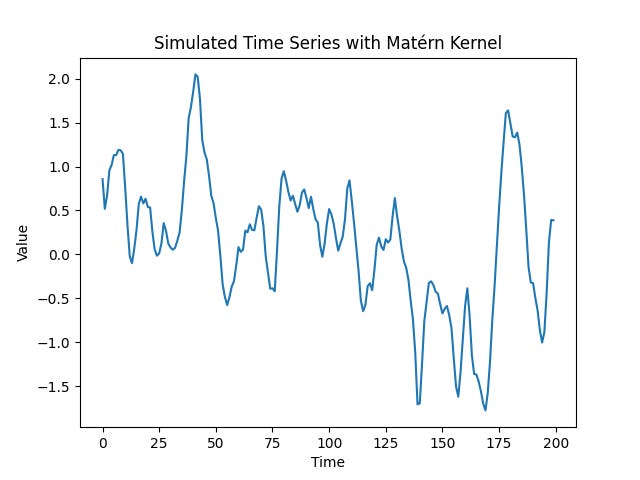
Synthetic Data

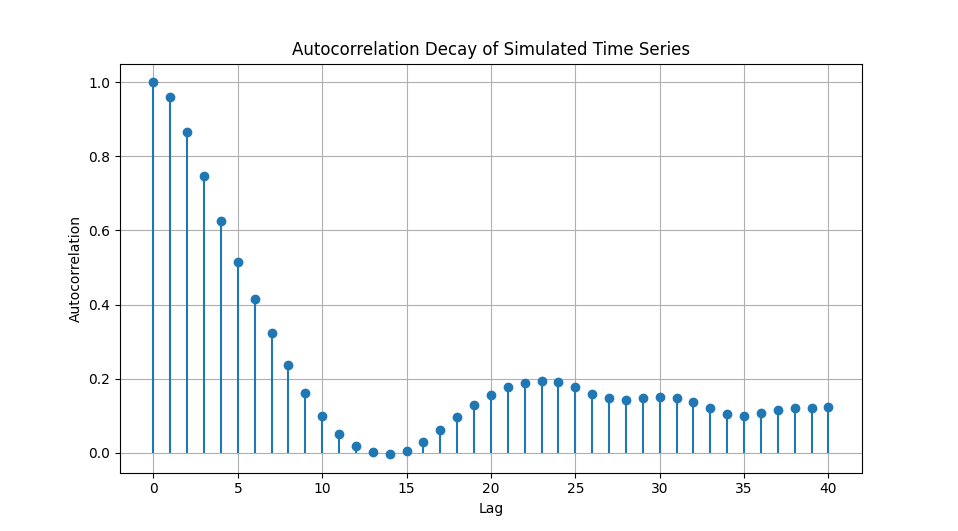
With a lengthscale argument of 1/3 the auto-correlation slowly decays away in a more power-law fashion indicative of long-range dependence. This mirrors the decaying gradient of auto-covariance seen in the matrix above.

auto-correlation decay plot

The smoothness parameter (nu) of 3/2 generates somewhat rougher data that is still once differentiable.

synthetic data from Matérn kernel

Data after differencing once.

synthetic data from Matern kernel

In future posts I will explore even more parameter combinations to demonstrate the flexibility of the kernel.

Python Implementation

def matern_covariance_matrix(
    time_series, 
    length_scale=1/3, 
    nu=3/2, 
    variance=1):
    """
    Compute the Matern auto covariance matrix for a 1D time series.
    
    Parameters:
    - time_series : array-like, shape (n_samples,)
        1D time series data points.
    - length_scale : float
        Length scale parameter rho in the kernel.
    - nu : float
        Smoothness parameter ν.
    - variance : float
        Variance (scale) parameter sigma^2.
        
    Returns:
    - mat : numpy.ndarray, shape (n_samples, n_samples)
        Matern covariance matrix (auto covariance).
    """
    time_series = np.atleast_1d(time_series)
    ts1 = time_series[:, None]
    ts2 = time_series[None, :]
    
    dists = np.abs(ts1 - ts2)
    
    dists_nozero = np.where(dists == 0, 1e-10, dists)
    
    factor = np.sqrt(2 * nu) * dists_nozero / length_scale
    
    coef = variance * (2**(1 - nu)) / gamma(nu)

    mat = coef * (factor**nu) * kv(nu, factor)
    
    np.fill_diagonal(mat, variance)
    
    return mat

References & Further Reading

Attention Is All You Need Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin

Attention is Kernel Trick Reloaded Gokhan Egri, Xinran (Nicole) Han

Implicit Kernel Attention Kyungwoo Song, Yohan Jung, Dongjun Kim, Il-Chul Moon

Sequence Transduction with Recurrent Neural Networks Alex Graves

Deep Kernel Learning Andrew Gordon Wilson, Zhiting Hu, Ruslan Salakhutdinov, Eric P. Xing, CMU, University of Toronto

Gaussian Process Scikit-Learn

Matern Kernel Scikit-Learn

Understanding Models and Model Bias with Gaussian Processes Kansas City Fed

& more in the README: https://github.com/regimelab/notebooks/